S.T.E.A.M. at Home: Fun with Food Part I – Triangle Discoveries
Twizzler Triangles and Pythagorean Cheez-Its
In these times of learning at a distance, many S.T.E.A.M. teachers have been caught off-guard. Not having uniform kits prepared for all of our students has made conducting a virtual S.T.E.A.M. course challenging. In this series, we are going to offer lesson ideas for the S.T.E.A.M. teacher that can be completed with students virtually, using items that can be found at home or acquired for a minimal cost. This is also an opportunity for children to get their parents involved in the learning process and raise awareness of your S.T.E.A.M. program. Our previous project focused on the students’ design capabilities as they scavenged for materials around their home in an attempt to build a raft. In this dual activity, we will examine triangles with the first triangle inequality theorem and the Pythagorean Theorem. According to the first triangle inequality theorem, the lengths of any two sides of a triangle must add up to more than the length of the third side. The Pythagorean Theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. This is a great activity that your students are sure to enjoy as it involves two tasty snacks.


Lesson Name: Fun with Food Part I: Triangle Discoveries (“Twizzler Triangles”)
Lesson Description: This lesson will help students identify the different types of triangles and determine the side measurements necessary to construct those triangles while attending to the first triangle inequality theorem.
Overview: The students will be shown pictures of different triangles based on their side lengths (scalene, isosceles, and equilateral). The scalene triangle as having no equal sides, an isosceles triangle as having at least two equal sides and an equilateral triangle as having all three sides equal. The Twizzler strips will be cut into various lengths and the students sort the strips by length and construct each of the triangle types you described.
S.T.E.A.M. Integration
Science: The science behind this lesson is the proving of the first triangle inequality theorem, which states that the lengths of any two sides of a triangle must add up to more than the length of the third side.
Technology: The technology is the method of how we cut the strips to the precise measurements.
Engineering: The engineering is in the types of triangles we can build.
Art: The art is in the sorting of the strips by size and or color if using different flavors of licorice.
Math: Mathematics enters this lesson with the measures that can and cannot be used to create a complete triangle by following the first triangle inequality theorem.
Extend-Expand-Explore: Have students spend time building as many triangles as possible and record what worked and what did not.
Lesson Plan
Title: Fun with Food Part I: Triangle Discoveries (“Twizzler Triangles”)
Objective: Students will learn how to salvage and repurpose recyclable materials into a floating device.
|
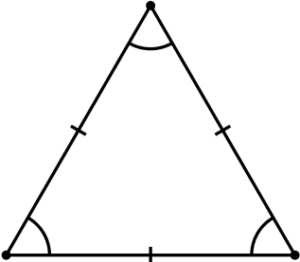
Equilateral Triangle (3 equal sides) |
|
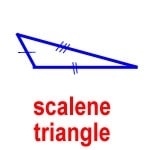
Scalene Triangle (No equal sides) |
|
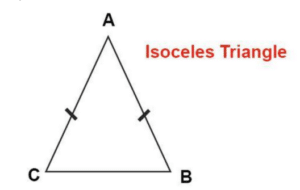
Isoceles Triangle (At least 2 equal sides) |
Materials: Twizzler candy strips, ruler, scissor
Procedure:
- Begin by showing the students pictures of different triangles based on their side lengths (scalene, isosceles, equilateral)
- Describe the scalene triangle as having no equal sides, an isosceles triangle as having at least two equal sides and an equilateral triangle as having all three sides equal.
- Next, have a guardian measure and cut several licorice strips into 1 inch, 2 inch, 3 inch, 4 inch, 5 inch, and 6 inch strips respectively.
- Have the students sort the strips by length and construct each of the triangle types you described.
- Now try to prove the first triangle inequality theorem. This rule states that the lengths of any two sides of a triangle must add up to more than the length of the third side. Students can prove this by attempting to build triangles with side measures like 1 inch, 2 inch, and 5 inch. They will see that this does not create a complete triangle. That is because 1 plus 2 equals 3 which is less than the third side of 5. Then try building a triangle with side measures of 3 inch, 4 inch, and 5 inch. This will create a triangle. That is because 3 plus 4 equals 7 which is greater than the third side 5.
Conclusion: Have a group discussion with the participants. Ask them to share a picture of their triangles with the group. Students can test out other measurements to see what works and what does not.
Lesson Name: Fun with Food Part I: Triangle Discoveries (“Pythagorean Cheez-Its”)
Lesson Description: This lesson will help students discover and prove the theorem of Pythagoras regarding the measures of the sides of a right triangle.
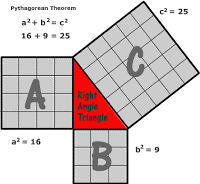
Overview: Students will build squares off of the two shorter legs of the right triangle. They will then count the total number of crackers it took to complete this task and use that number to complete a square off the longest side of the right triangle.

S.T.E.A.M. Integration
Science: The science behind this lesson is in the discovery of the Pythagorean Theorem.
Technology: The technology that makes this project work is the use of the Cheez-it cracker as a unit of measure.
Engineering: The engineering is not only in the ability to construct additional right triangles besides the introductory 3-4-5 triangle and thereby discovering more Pythagorean triples.
Art: The art is in the design of the placemat with the Pythagorean worksheet.
Math: Mathematics enters this lesson with the measures of the triangle sides as well as the measuring of a right angle and writing and solving and equation for the Pythagorean Theorem.
Extend-Expand-Explore: Have students explore more Pythagorean triples like 6-8-10 and 5-12-13. Work the Pythagorean Theorem in reverse by giving the hypotenuse and one side and solving for the missing side.
Lesson Plan
Title: Fun with Food Part I: Triangle Discoveries (“Pythagorean Cheez-Its”)
Objective: Students will be able to prove the theorem of Pythagoras – a rule about right triangles that is thousands of years old.
Materials: Cheez-it crackers, placemat, Pythagorean triangle worksheet
Procedure:
- Distribute the 3-4-5 Pythagorean worksheet (see below) and instruct students to print it and mount it to a placemat, which they can customize.
- Have students line up three Cheez-it crackers along the 3-side of the triangle. Then ask them to complete building that square. Ask how many crackers it took to complete the square. The answer is nine.
- Next have students line up four Cheez-it crackers along the 4-side of the triangle. Then ask them to complete building that square. Ask how many crackers it took to complete the square. The answer is 16.
- Now add the 9 crackers and 16 crackers from the previous two steps. The sum is 25.
- Take these 25 crackers and use them to build the last square off of the 5-side of the triangle. You will see it takes exactly 25 crackers to complete.
Conclusion: Have a group discussion with the participants. Ask them to explain what they have discovered about the Pythagorean Theorem. Ask them to name some multiple of the 3-4-5 triangle that could be easily created with the crackers.