Writing Across the Curriculum: Descriptive Problem-Solving in Your Math Class
Most of the time spent in the typical mathematics classroom is dedicated to preparing for standardized testing. We tend to teach to the test and focus on those skills necessary for our students to excel. However, one of the skills that tends to get lost is the art of problem solving. Multi-layered problems that hinge upon previous steps or those that ask for the process to be explained can become a truly challenging obstacle for both the students trying to learn and the teachers trying to explain it. Unfortunately, there is no formula that works for all problems. On the bright side, there is something we as teachers can do and that is give our students the opportunities to solve problems that require critical thinking and explanation of their reasoning. We can do this by asking them to write in the mathematics classroom. Writing is often left to the language arts classroom, but there is no rule that says it cannot become a staple in that mathematics classroom as well.
The following are a series of problems that require the student to read the problem, establish a plan, execute that plan, and then explain their strategy in words.
Problem 1: Now that school has begun, students are deciding what extra-curricular activities they want to try. Students are involved in soccer, student council, math club, and basketball in a ratio of 6:3:2:4 respectively. There are 180 students eligible for one of these activities. For the purpose of this problem, no single student is involved in more than one activity, and everyone is involved in something. Based on this ratio, how many students are involved in the math club? Please show your work and explain (in complete sentences) how you arrived at your answer.
| Soccer | Student Council | Math Club | Basketball | |
| Ratio | 6 | 3 | 2 | 4 |
| Actual |
Solution 1: The key to this problem is to add the ratios (6+3+2+4 = 15) and then divide that into the total 180 students. 180/15=12. Twelve becomes the scale factor by which each category must be multiplied.
| Soccer | Student Council | Math Club | Basketball | |
| Ratio | 6 | 3 | 2 | 4 |
| Actual | 6 x 12 = 72 | 3 x 12 = 36 | 2 x 12 = 24 | 4 x 12 = 48 |
The question asked specifically for the number of students in the math club, which is 24.
Problem 2: Have you ever noticed how kids climb stairs? They can go up one step at a time if they are carrying a heavy backpack or, if they are in a rush, they can skip up two steps at a time. However, what if you could climb the stairs using combinations of one and two steps? Mixing and matching the ones and twos, how many ways would there be to add up to the ten steps? {For example, I could climb the stairs like this: 1+1+1+1+1+1+1+1+1+1=10 or 2+2+2+2+2= 10 or 1+2+2+1+1+1+2 = 10}.
Solution 2:
| Number of Steps | How to Climb | Number of Ways |
| 1 | 1 | 1 |
| 2 | 1+1 or skip (2) | 2 |
| 3 | 1+1+1, 2+1, or 1+2 | 3 |
At this point, you might be saying that one step has one way to climb it, two steps have two ways to climb, three steps have three ways to climb and so on. However, let’s take a look at what happens when we get to four steps.
| 4 | 1+1+1+1, 2+2, 1+1+2, 2+1+1, 1+2+1 | 5 |
The pattern took a turn and now shows five ways. Let’s try one more.
| 5 | 1+1+1+1+1, 2+1+1+1, 1+1+1+2, 1+2+1+1, 1+1+2+1, 2+2+1, 1+2+2, 2+1+2 | 8 |
You can see that it gets progressively harder to list the ways to climb the steps, so let’s see if we can find a pattern. Look at the column titled “Number of Ways”.
| Number of Ways |
| 1 |
| 2 |
| 3 |
| 5 |
| 8 |
| 13 |
| 21 |
| 34 |
| 55 |
| 89 |
Did you notice that every time we increase the number of steps, the number of ways is increased by the number of ways in the cell above it? For instance, 1+2=3; 2+3=5; 3+5=8; 5+8=13; 8+13=21; etc. Here we have the makings of a Fibonacci sequence. Therefore, by the time we get to ten steps, there are 89 ways to climb them using only one and two steps at a time.
Problem 3: Twenty people have gathered and are meeting for the first time. Each person has to introduce themselves to every other person by shaking their hand. If two people meet, one handshake occurs. So how many handshakes would occur if there were twenty people in the room? {Arrows represent a handshake}
Solution 3:
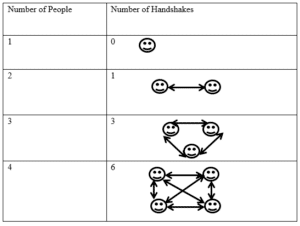
So as you can see, it gets progressively more difficult to draw the diagrams as we add more and more people. So let’s look for a pattern. Begin by focusing on the “Number of Handshakes” column. Did you notice the gaps between the numbers? (0 + 1 = 1; 1 + 2 = 3; 3 + 3 = 6 and so on) The addition goes +1, +2, +3, etc. So now, let’s complete the chart.
| Number of People | Number of Handshakes |
| 1 | 0
+1 |
| 2 | 1
+2 |
| 3 | 3
+3 |
| 4 | 6
+4 |
| 5 | 10
+5 |
| 6 | 15
+6 |
| 7 | 21
+7 |
| 8 | 28
+8 |
| 9 | 36
+9 |
| 10 | 45
+10 |
| 11 | 55
+11 |
| 12 | 66
+12 |
| 13 | 78
+13 |
| 14 | 91
+14 |
| 15 | 105
+15 |
| 16 | 120
+16 |
| 17 | 136
+17 |
| 18 | 153
+18 |
| 19 | 171
+19 |
| 20 | 190 |
We therefore have 190 handshakes occurring when there are 20 people in the room.
Problem 4:
The students in your school are having a friendship-gram card sale. They have 1,000 friendship-grams to sell. In order to be ready for the customers, they want to have the friendship-grams in the envelopes organized in such a way that a customer can ask for any quantity of friendship-grams between 1 and 1,000 inclusive and the students would be able to give that exact number simply by handing the customer a certain combination of pre-loaded envelopes. They will mark the outside of the envelopes as to how many friendship-grams they contain, but they will not be able to add or subtract friendship-grams from the envelopes once they are inside. Please mark the envelopes below to show how they should be set up and explain any pattern you discover. [Hint: the pattern will break at the last envelope due to the 1,000 friendship-gram limit]

Solution 4:
The least amount of cards that can be requested is one, so we know that we must have an envelope containing one card.

The next amount that could be requested is two, so we have a decision to make. Do we place another single card in the envelope or do we have an envelope containing two? The better choice is to have two. The reason is that now we can create 1, 2, and even three cards by adding our existing envelopes so far.
Now that we are covered up to 3 cards, we need to make a 4. We can do this a number of different ways, but the best choice is to place 4 cards in the next envelope. That way we can combine cards at this point to make a 1, 2, 3, 4, 5, 6, and even a 7 simply by adding different combinations of what we have. Then next number we need to create is 8, so we should place 8 cards in the next envelope. Hopefully, by now you start to realize that we are doubling the number of cards each time we get to the next envelope.

Now you might be saying that if we keep doubling then the last envelope should contain 512 cards. However, we must remember the 1,000 card limit. So at this point, if we total the number of cards we have now, it’s 489. Subtract 489 from 1,000 leaves 511 cards in our last envelope.

It is my hope that you have enjoyed these sample problems and share them with your students and your colleagues. Create a library and add more critical thinking questions. They can be used as ice-breakers or extra credit.





