Popcorn Predictions: An Integrated S.T.E.M. Lesson

Popcorn Predictions: An Integrated S.T.E.M. Lesson

Overview

Our previous project incorporated a chemical change which used the acid in vinegar to release the gas from baking soda. This time we will turn our attention to a physical change. In this lesson we will use sample data to make a prediction as to the volume of a container. This is an enjoyable project that you might consider inviting your class parents to participate in as you promote your S.T.E.M. program.

This lesson works well in your S.T.E.M. Lab on a budget and is appropriate for grades 4-6. You will need popcorn kernels (un-popped), hot air poppers, measuring cups, construction paper, tape, scissors, zip-lock bags, bowls, and rulers.

In preparation for the lesson, you will need to count out 200 kernels of corn for each group. This is a good task to give to students groups. Place the counted kernels into zip-lock bags. Next, pop ten kernels of corn and have students examine the amount of space occupied by 10 popped kernels. Have students make and record a prediction for how much space 200 popped kernels would require. Next, students will build a container to hold the predicted volume of popped corn using the construction paper and tape. The goal is to construct a container to most closely hold the popped corn without being over or under-sized. Now pop the 200 kernels for each group and have them test their containers’ volumes. You can turn this into a contest and the winner would be determined by which group has most accurately predicted the exact volume.

Science

We witnessed a physical change. Applying heat to the un-popped corn caused the tiny amount of water inside it to turn into steam. When the pressure builds and the shell of the corn can no longer hold together, the kernel pops as a result of the pressure.

Technology

The technology behind this project is in the premise that we can use different container shapes to hold the same volume. This is a good practical example because in a real-word situation, it might be more convenient or efficient to have a different shape – especially when stacking containers. We can even experiment with different popping technologies to see which is most efficient like traditional oil in a pot or microwaveable types. In our experiment, efficiency is measured by how many un-popped kernels are left afterwards. The fewer un-popped kernels left, the more efficient the mechanism.

Engineering

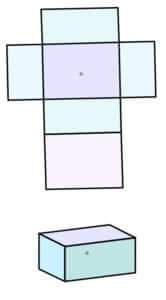
The engineering is in the design and construction of our popcorn containers. Containers could be rectangular prisms, pyramids, cones, cubes, or some other 3-dimensional shape. It may be more difficult to predict the capacity of a container that tapers to a point. Groups should be encouraged to sketch their container on paper and create the “net” for their 3-dimensional container. The “net” is the flattened, unfolded shape and serves as the blueprint for the design.

Mathematics

The mathematics behind the scenes is the use of the various volume formulas that would be used to calculate the capacity of the containers. Volumes for right-angled objects are found by multiplying the area of the base by the height. The variations in the formulas will occur depending on what shape composes the base (square, rectangle, circle, etc.). The volumes for objects that come to a point are found by taking one-third of the area of the base multiplied by the height.

Extend-Expand-Explore

Extend the lesson to explore different dimensions and/or different objects that produce the same volume. Change up the lesson by altering the total number of kernels of corn you want to accommodate in your container as well as the number of popped kernels you use to make the prediction. Expand the lesson to incorporate statistics by examining the amount of un-popped kernels of corn and create a margin of error. Also, explore different popcorn popping technologies that may reduce the amount of un-popped kernels.

Lesson Plan

Title: Popcorn Predictions

Objectives: To make prediction estimates based on a sample

Materials:

• popcorn kernels (un-popped)
• hot air poppers
• measuring cups
• construction paper
• tape
• scissors
• rulers
• zip-lock bags
• bowls

Procedure:

1. count out 200 kernels of corn
2. count out and pop 10 kernels of corn
3. have students examine the amount of space occupied by 10 popped kernels
4. have students make a prediction for how much space 200 popped kernels would require
5. students then build a container to hold the predicted volume of popped corn using construction paper and tape
6. Project goal is to construct a container to most closely hold the popped corn without being over- or under- sized
7. pop the 200 kernels for each group and have them test their container capacity

Conclusion:

Have student groups examine each other’s containers. Who was closest?

Is it possible to have to different shaped containers that hold the same volume?

What are some problems with making predictions? How can we account for these errors?

• Christopher Masullo, Ed.D.